Reprint from Master Handbook of Acoustics
The popularity of rectangular rooms is due in part to economy of construction, but is has its acoustical advantages. The axial, tangential, and oblique modes can be calculated with reasonable effort and their distribution studied. For a first approximation, a good approach is to consider only the more dominant axial modes, which is a very simple calculation. Degeneracies (mode pile-ups) can be spotted and other room faults revealed.
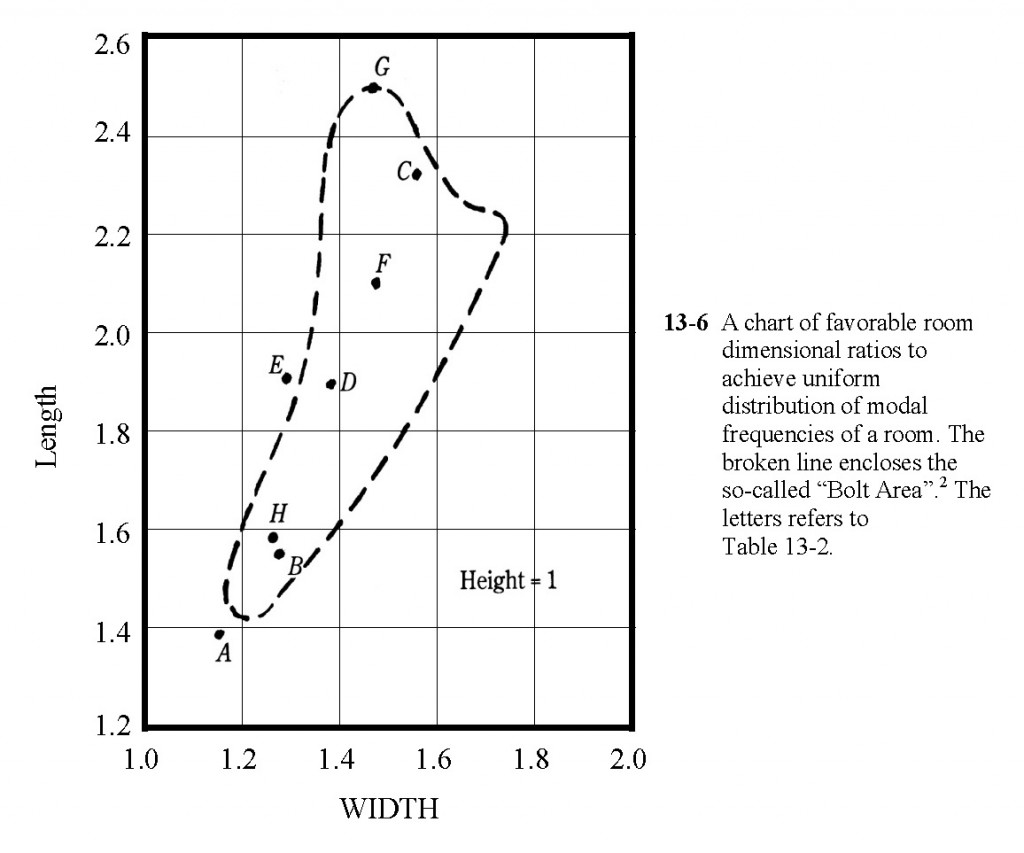
The relative proportioning of length, width, and height of a sound sensitive room is most important. If plans are being made for constructing such a room, there are usually ideas on floor-space requirements, but where should one start in regard to room proportions? Cubical rooms are anathema. The literature is full of early quasi-scientific guesses, and later statistical analyses of room proportions that give good mode distribution. None of them come right out and say, “This is the absolute optimum.” Bolt2 gives a range of room proportions producing the smoothest room characteristics at low frequencies in small rectangular rooms (Fig. 13-6). Volkmann’s 2:3:5 proportions,3 was in favor fifty years ago. Boner suggested the 1 : 1.26 : 1.59 ratio as optimum.4 Sepmeyer5 published a computer statistical study in 1965 that yields several favorable ratios. An even later paper by Louden6 list 125 dimension ratios arranged in descending order of room acoustical quality.